Java二叉搜索樹基礎原理與實現方法詳解
本文實例講述了Java二叉搜索樹基礎原理與實現方法。分享給大家供大家參考,具體如下:
前言:本文通過先通過了解一些二叉樹基礎知識,然后在轉向學習二分搜索樹。
1 樹1.1 樹的定義樹(Tree)是n(n>=0)個節點的有限集。n=0時稱為空樹。在任意一顆非空樹中:
(1)有且僅有一個特定的稱為根(Root)的節點;(2)當n>1時,其余節點可分為m(m>0)個互不相交的有限集T1、T2、......、Tn,其中每一個集合本身又是一棵樹,并且稱為根的子樹。此外,樹的定義還需要強調以下兩點:(3)n>0時根節點是唯一的,不可能存在多個根節點,數據結構中的樹只能有一個根節點。(4)m>0時,子樹的個數沒有限制,但它們一定是互不相交的。
下圖為一棵有10個節點的一般樹的結構:
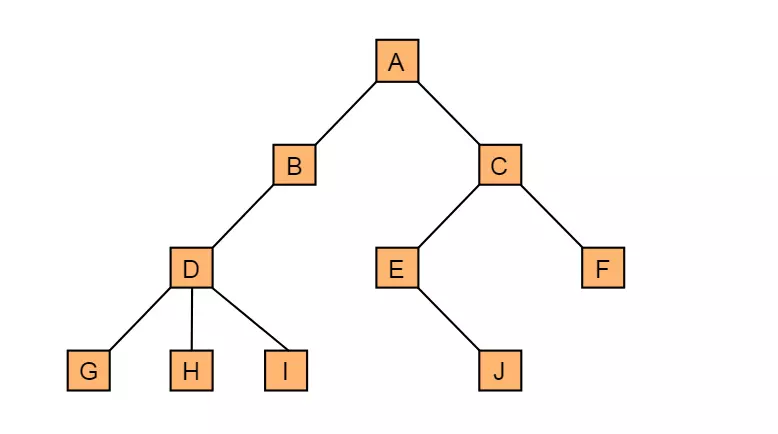
由樹的定義可以看出,樹的定義使用了遞歸的方式。遞歸在樹的學習過程中起著重要作用。
2 二叉樹2.1 二叉樹定義二叉樹是n(n>=0)個節點的有限集合,該集合或者為空集(稱為空二叉樹),或者由一個根節點和兩棵互不相交的、分別稱為根節點的左子樹和右子樹組成。圖2.1展示了一棵一般二叉樹結構:
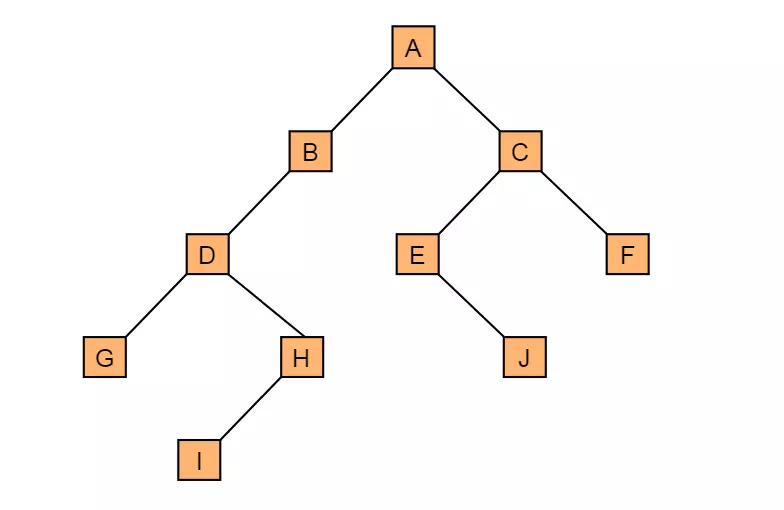
由二叉樹定義以及圖示分析得出二叉樹有以下特點:
(1)每個節點最多有兩顆子樹,所以二叉樹中不存在度大于2的節點。(2)左子樹和右子樹是有順序的,次序不能任意顛倒。(3)即使樹中某節點只有一棵子樹,也要區分它是左子樹還是右子樹。二叉樹是動態的數據結構
可以用一下代碼來表示一個樹節點:
class Node<E>{ E e; Node left; Node right;}
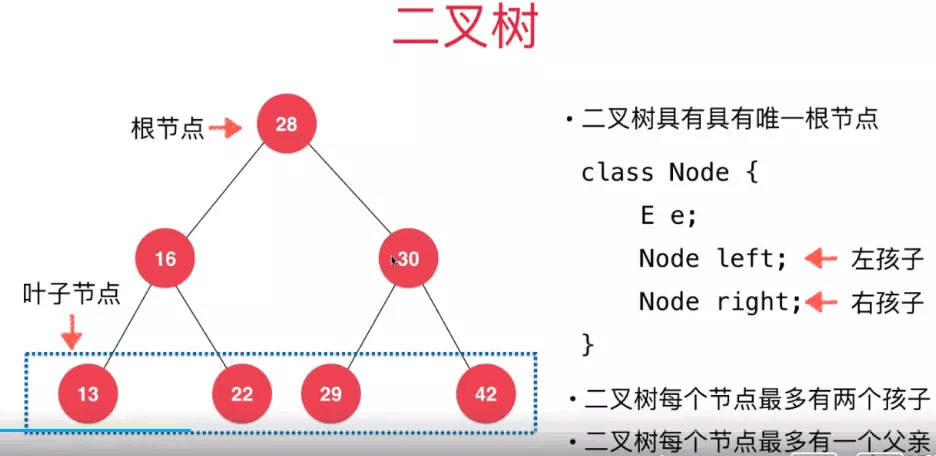
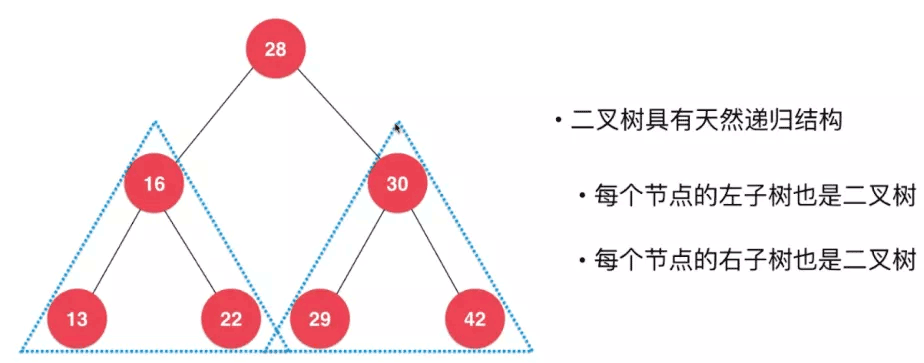
1.二叉樹具有天然的遞歸結構
這是由于,每個節點的左子樹與右子樹都是二叉樹(有的情況下),如圖:
類型2:
類型3:
類型4:
類型5:

二叉查找樹(Binary Search Tree),也稱有序二叉樹(ordered binary tree)、排序二叉樹(sorted binary tree),是指一棵空樹或者具有下列性質的二叉樹:
1.若任意節點的左子樹不空,則左子樹上所有結點的值均小于它的根結點的值;2.任意節點的右子樹不空,則右子樹上所有結點的值均大于它的根結點的值;3.任意節點的左、右子樹也分別為二叉查找樹。4.沒有鍵值相等的節點(no duplicate nodes)。
因此使用二叉樹存儲的元素必須有可比性。
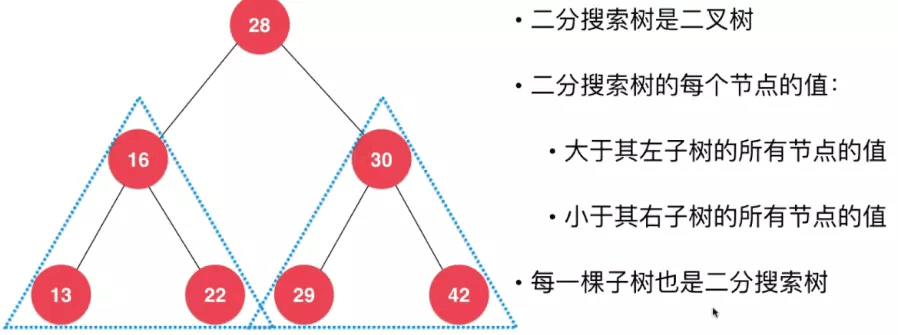
二叉查找樹本質上是一種二叉樹,所以上章講的二叉樹的性質他都有。
3.3二分搜索樹的思想:二叉排序樹的查找過程和次優二叉樹類似,通常采取二叉鏈表作為二叉排序樹的存儲結構。中序遍歷二叉排序樹可得到一個關鍵字的有序序列,一個無序序列可以通過構造一棵二叉排序樹變成一個有序序列,構造樹的過程即為對無序序列進行排序的過程。每次插入的新的結點都是二叉排序樹上新的葉子結點,在進行插入操作時,不必移動其它結點,只需改動某個結點的指針,由空變為非空即可。搜索,插入,刪除的復雜度等于樹高,O(log(n)),后續逐一進行學習。
4.編程實現二叉搜索樹4.1 基礎代碼由于使用二叉樹存儲的元素必須有可比性,因此在實現時需要BST類繼承Comparable。
package BST;public class BST<E extends Comparable<E>> { //定義樹節點 private class Node { public E e; public Node left, right; public Node(E e) { this.e = e; left = null; right = null; } } private Node root;//根節點 private int size; public BST() { root = null; size = 0; } //二分搜索樹存儲元素個數 public int size() { return size; } //二分搜索樹存儲元素是否為空 public boolean isEmpty() { return size == 0; }}
本節算是二叉搜索樹的一個入門,后續將繼續完善、更新。
更多關于java算法相關內容感興趣的讀者可查看本站專題:《Java數據結構與算法教程》、《Java操作DOM節點技巧總結》、《Java文件與目錄操作技巧匯總》和《Java緩存操作技巧匯總》
希望本文所述對大家java程序設計有所幫助。
相關文章:

 網公網安備
網公網安備