python編寫softmax函數、交叉熵函數實例

python代碼如下:
import numpy as np # Write a function that takes as input a list of numbers, and returns# the list of values given by the softmax function.def softmax(L): pass expL = np.exp(L) sumExpL = sum(expL) result = [] for i in expL: result.append(i*1.0/sumExpL) return result
python編寫交叉熵公式:
import numpy as np def cross_entropy(Y, P): Y = np.float_(Y) P = np.float_(P) return -np.sum(Y * np.log(P) + (1 - Y) * np.log(1 - P))
補充知識:分類時,為什么不使用均方誤差而是使用交叉熵作為損失函數
MSE(均方誤差)對于每一個輸出的結果都非常看重,而交叉熵只對正確分類的結果看重。
例如:在一個三分類模型中,模型的輸出結果為(a,b,c),而真實的輸出結果為(1,0,0),那么MSE與cross-entropy相對應的損失函數的值如下:
MSE:
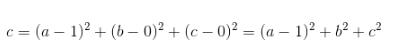
cross-entropy:
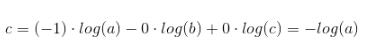
從上述的公式可以看出,交叉熵的損失函數只和分類正確的預測結果有關系,而MSE的損失函數還和錯誤的分類有關系,該分類函數除了讓正確的分類盡量變大,還會讓錯誤的分類變得平均,但實際在分類問題中這個調整是沒有必要的。
但是對于回歸問題來說,這樣的考慮就顯得很重要了。所以,回歸問題熵使用交叉上并不合適。
以上這篇python編寫softmax函數、交叉熵函數實例就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持好吧啦網。
相關文章:

 網公網安備
網公網安備